Understanding the A star algorithm
I recently learnt about the workings of the A* algorithm through Udacity's Intro to Self Driving Cars Nanodegree, and wanted to understand it in detail, hence this post on it.
Wikipedia article on A* states: "A star is a computer algorithm that is widely used in pathfinding and graph traversal, which is the process of finding a path between multiple points, called "nodes". It enjoys widespread use due to its performance and accuracy."
It was devised by Peter Hart, Nils Nilsson and Bertram Raphael of Stanford Research Institute (now SRI International) who first published the algorithm in 1968.
Table of Contents
Setup¶
We have a map of interconnected nodes and the problem that we want to solve is to find the shortest path between two nodes.
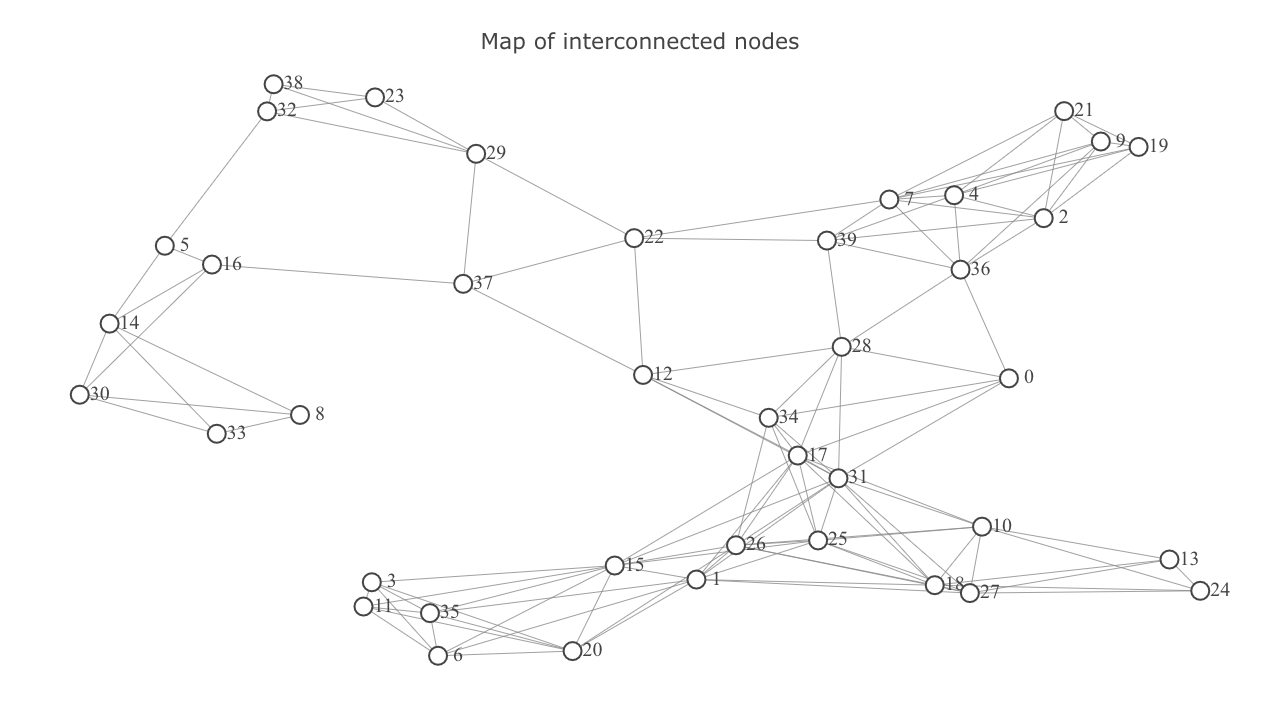
Terminology¶
Let's define some terminology that will help us understand the algorithm.
- Initial state () in the case of route finding refers to being at a starting node.
-
Actions ->
It refers to producing outcomes for a particular state. eg. the possible actions for the state of being at node
8are movement to nodes14,30, and33. -
Result ->
The combination of being in a particular state and taking a particular action produces a new state. eg. the state of being at node
8and action of moving to node14results in the state of being at node14with it's own set of further possible actions. - Step Cost refers to the cost incurred in taking an action. In the case of route finding, it can be the distance travelled while going from one node to another.
- Path Cost is the summation of individual step costs along a path consisting of one or more nodes.
- State Space is the set of all states we can be in. We navigate the state space by applying actions.
The A-star Algorithm¶
Let's start understanding these concepts using the map shown above. Let's use node 8 as start goal and node 2 as goal node.
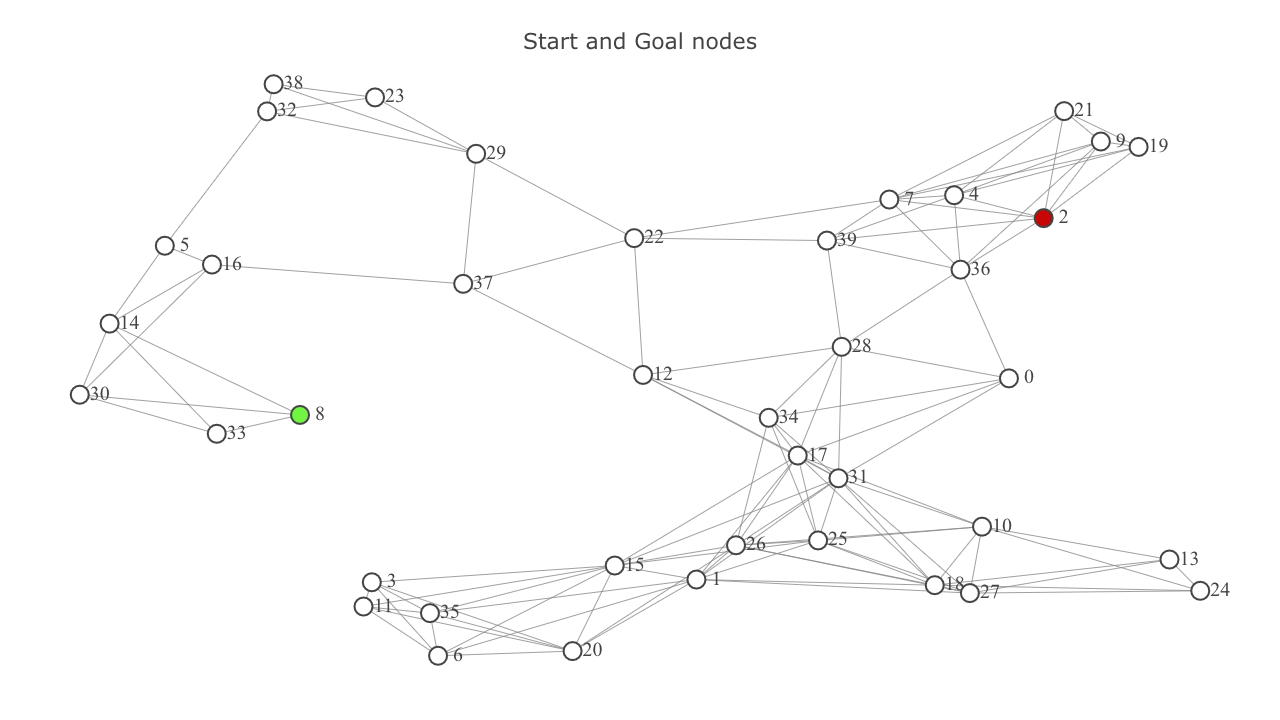
A* uses a metric called f-score which is a score to gauge how fruitful moving to the neighbor will be in finding the optimal path.
where is the f-score, or g-score is the path cost of a node, and h is a heuristic used to estimate distance between a node and the goal. In this case, we'll be using euclidian distance between two nodes as the heuristic.
Currently, the g-score of node 8 is zero while that of all others is set to infinity (as we don't have that knowledge yet). As a result, the f-score of all nodes except 8 is infinity. f-score of 8 is just the value of for 8.
To make our lives easier we'll divide up the state space into separate segments:
- Explored
- Frontier
- Unexplored
We'll start with the frontier consisting just the start node. Until the frontier is empty or we reach the goal node, we'll do the following:
- Choose the node with the lowest
f-score. At this moment it's node8. Let's call this node thecurrentnode. - If the
currentnode is thegoalnode, we're done. If not, remove it from thefrontierand add it to theexploredset. - Start exploring the neighbors of the
currentnode. representscurrentnode, and represents the neighbor being considered.
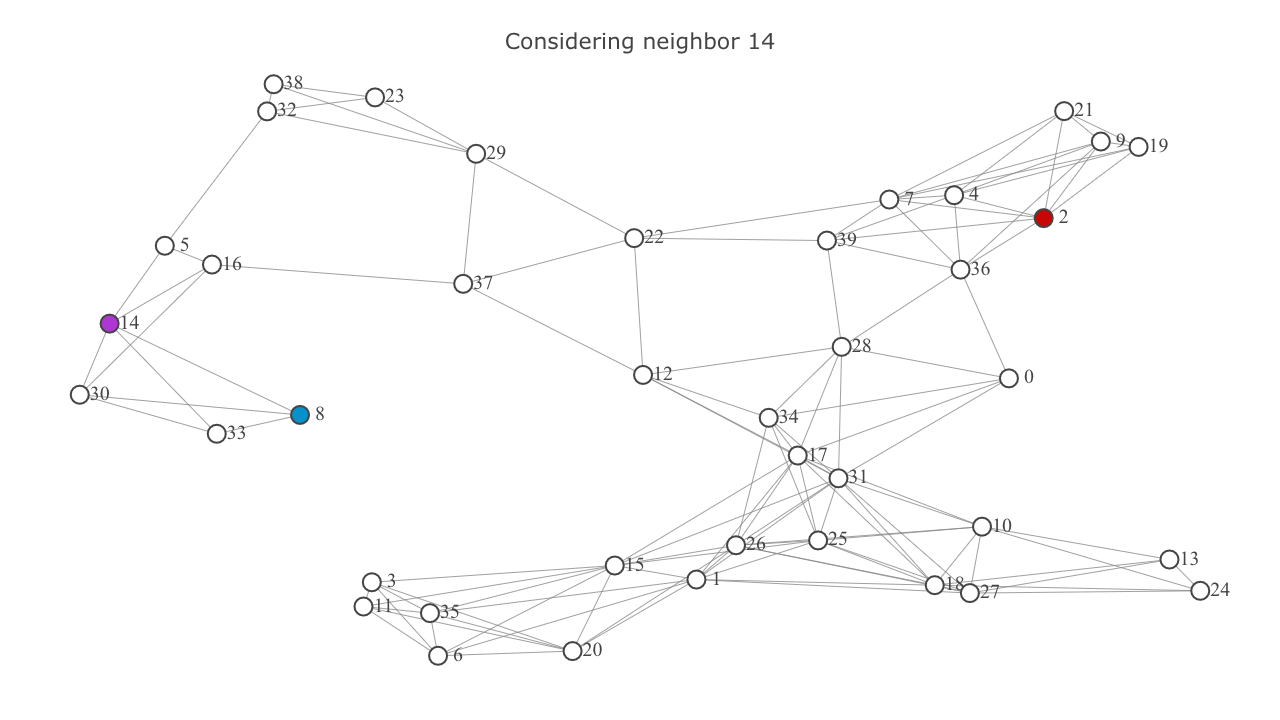
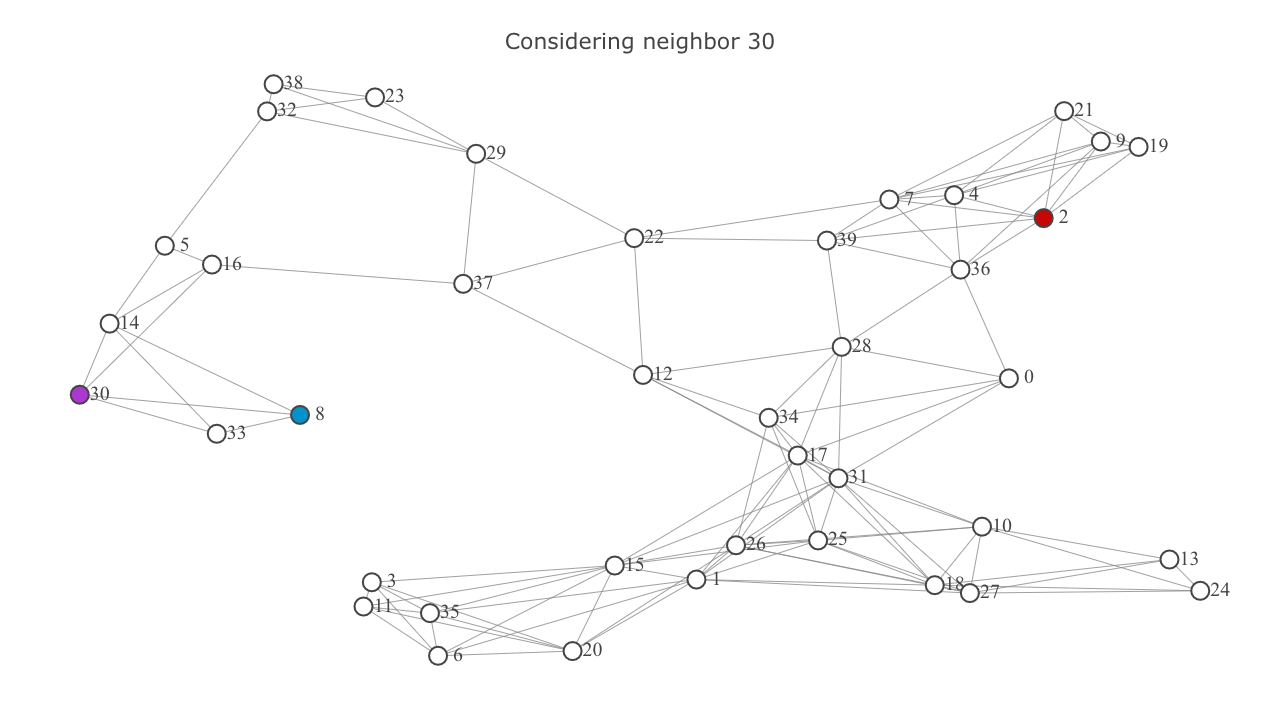
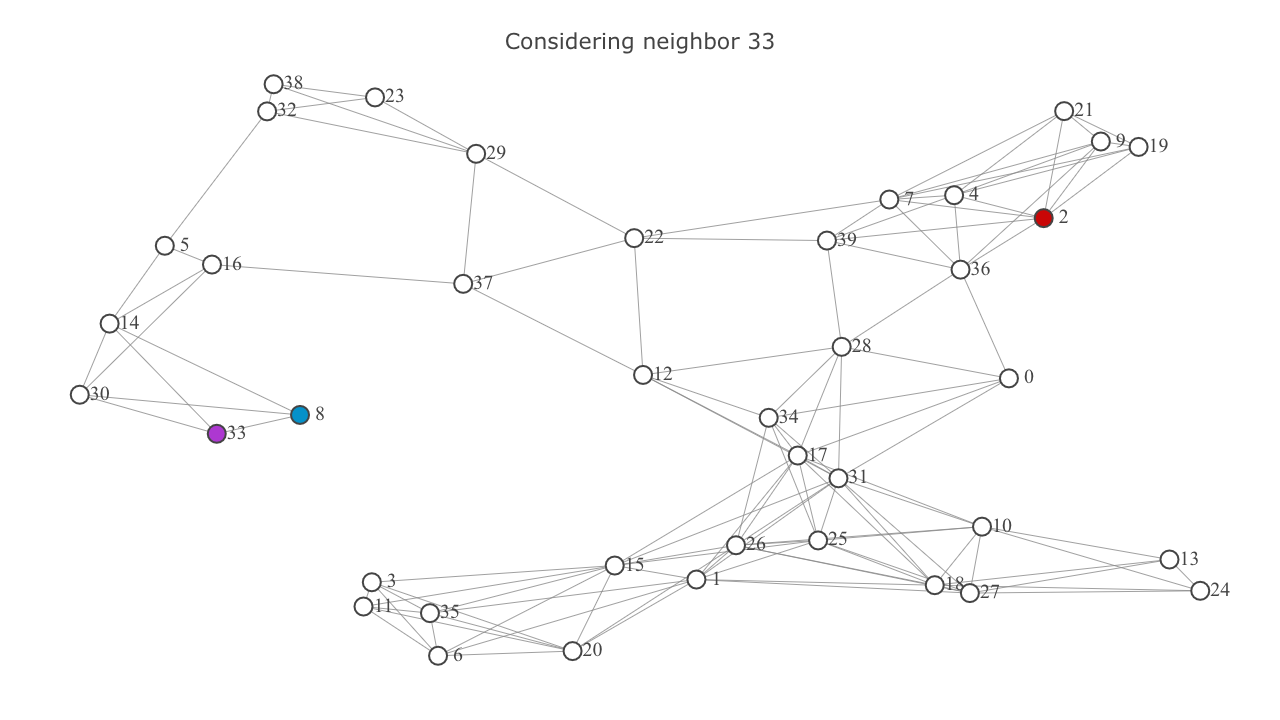
- Add each neighbor to the
frontierif it's not already in it. Ignore the neighbor if it's in theexploredset. This will be highlighted below in the video frames titled "Already explored: {node}". - In the former case (ie, if the neighbor wasn't in the
exploredset), calculate it's tentativeg-score. In this case the tentativeg-scoreis the sum of theg-scoreofcurrentand the euclidian distance betweencurrentand the neighbor. Set the neighbor'sg-scoreas this tentativescore. Also update the neighbor'sf-score.
This is how the map looks after one iteration of exploration. represents the frontier set.
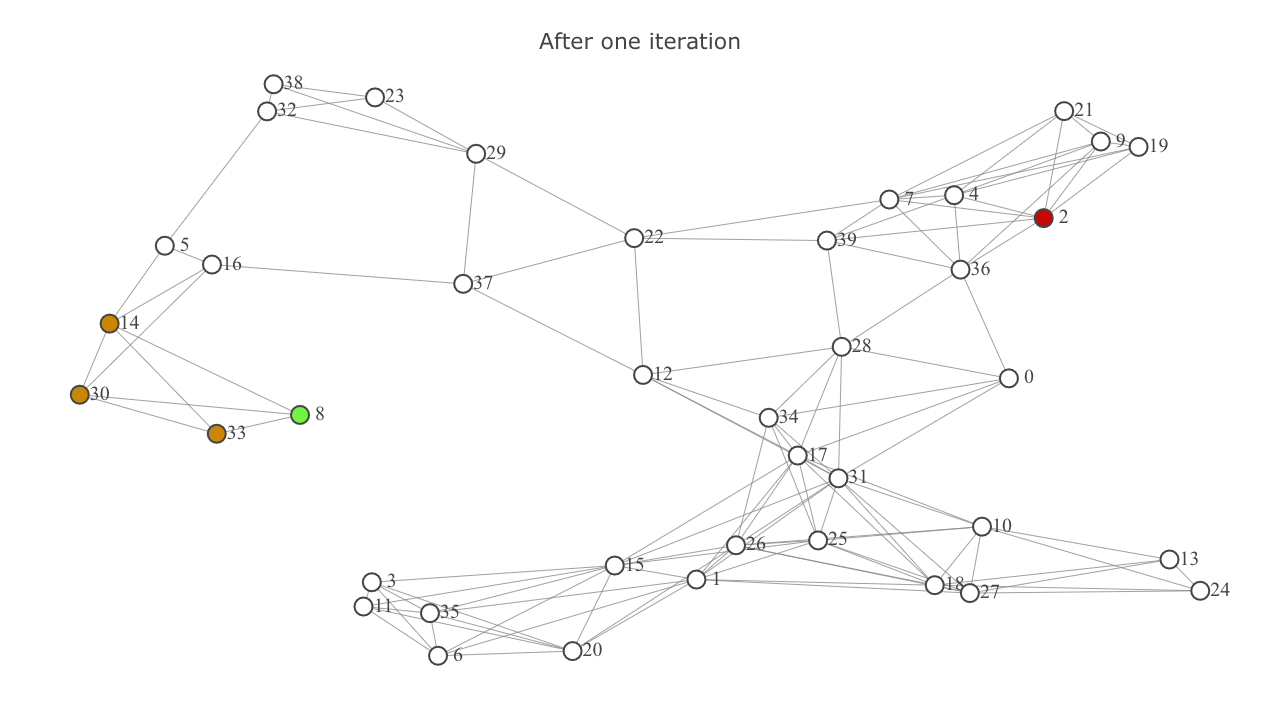
- Now we repeat the above steps again. This time the node with the lowest f-score will be
33. - One point to take note here is that if the tentative
g-scoreof a neighbor node is greater than or equal to it's already calculatedg-score, there exists a better route to the neighbor than the path being considered. This will be highlighted below in the video frames titled "Better route exists to: {node}".
This is how the map looks after second iteration. The explored set is indicated by and includes the nodes 8 and 33. (8 is highlighted as since it's the start node).
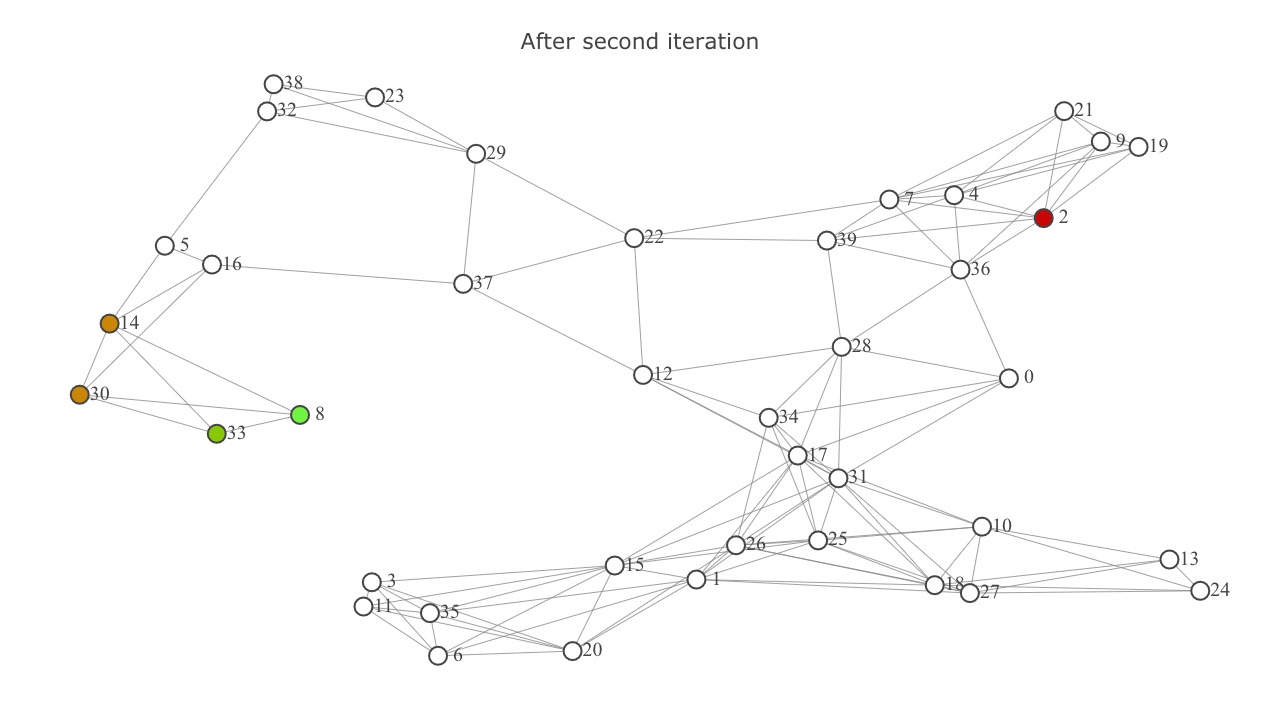
This is how things look after the third iteration.
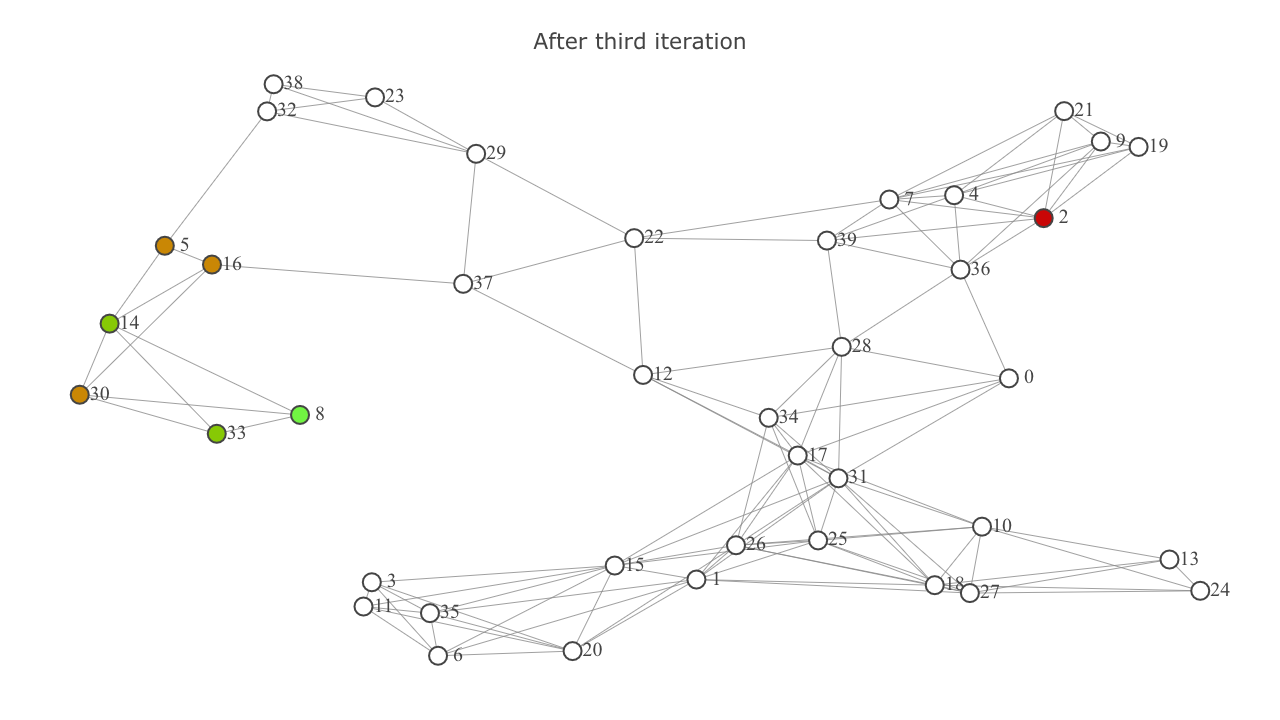
A-star summed up¶
- Start with the frontier consisting of a single node, which is the start node.
- Set up
g-scores for all nodes toinfinityexcept the start node, which is set tozero. As a result,f-scores for all nodes except the start node is alsoinfinity. - While there are nodes in the frontier, in each iteration, choose the node with the lowest
f-score. Term it ascurrentnode for the current iteration. - Go through each of this node's neighbors, and update it's
g-scoreandf-scoreusing the formula where is the path cost of the neighbor (from the start node), and is the heuristic. Ignore the neighbor if it's already in thefrontieror theexploredset. Also ignore the neighbor if the tentativeg-scoreof neighbor (g-scoreof "current node" + euclidian distance between "current node" and the neighbor) is greater than or equal to theg-scoreof the neighbor. (This means that there exists a shorter route to the neighbor than the current route being considered). - Repeat last two steps until the
currentnode is the goal node, or the frontier is empty.
Demo¶
Below is a video which shows the implementation of A* for finding shortest route between nodes 8 and 2.
represents the start node.
represents the goal node.
represents nodes in the frontier set.
represents nodes in the explored set.
represents current node, ie, the node with the lowest f-score.
represents neighbors of the current node being considered for exploration.
Shortest route between nodes 20 and 22:
Shortest route between nodes 38 and 21:
Code for the implementation can be found here.